「日本の金利が上がるわけない」「日本でインフレはあり得ない」
普通に考えると間違ってないと思いますが、悪いインフレが起こる可能性はそれなりにあると思います。
悪いインフレの場合、想像を超える上昇になる可能性もあります。
住宅ローンを変動金利で借りている場合、リスクが急に顕在化することになります。
詳細は下記をご覧ください。
変動金利ローンは金利が低く魅力的だが日本は悪い金利上昇の可能性もあるので注意が必要
住宅ローンを変動金利で借りている方が多いようです。
2020年時点で変動金利を選択した場合、借入金利は0.5%前後と非常に低い水準です。
例えば3,000万円を期間30年で借りた場合、金利が上昇せず0.5%のまま推移したと仮定すると支払総額は3,231万円です。
30年借りて利息はだったの231万円です。
これは確かに魅力的です。
さらに住宅ローンは元利均等払いですので、金利が低いと元金の返済割合が高くなり合理的といえます。
ただし、金利上昇には注意が必要です。
超低金利があまりにも長く続きすぎて、「金利なんてもう上がらないだろう」と持っている人も多いと思います。
経済が成熟化していることや基本的にデフレ体質な点を考えると、一般的には極端な金利上昇は考えにくいと思うでしょう。
しかし、日本の場合、「悪いインフレ」が起こるリスクはゼロではありません。
財政問題は悪化する一方です。
日銀は債券のみならず、中央銀行では唯一、株式(ETF)やJ-REITまで購入しています。
現在は日本は破綻しないという前提でマーケットの取引が行われていますが、この前提が揺らぐと少し雰囲気が変わってきます。
日本の財政が破綻するリスクの高まりや日銀の信認の低下が注目され始めると債券や通貨が売られる可能性がでてきます。
そうなると金利が上昇し、円安が進みます。
そして株式も売られることになります。
いわゆる株式・債券・通貨のトリプル安です。
通常のマーケットではこの現象は中々発生しません。
円安になれば日本株は上がりますし、株価が下がるような環境で金利は上がりません。
日本が破綻しないという前提がある限り、大規模なトリプル安は起こりません。
しかし、今の日本の現状をみると先進国で初の大規模トリプル安が発生してもおかしくありません。
しかも、悪いインフレの場合、一度発生すると現在では想像できない水準まで金利が上昇するリスクがあります。
短期金利が4%、5%の可能性も出てきます。
- 政府債務残高の推移はこちらをご覧下さい:世界の政府債務残高(対GDP比)/世界の政府純債務残高(対GDP比)推移
- 日銀の国債・株式・J-REITの買入れ状況はこちらをご覧下さい:日銀の国債・日本株ETF・J-REIT買入れ金額の変遷とバランスシート残高
少し長くなりましたが、金利が予想以上に上昇する可能性はゼロではありません。
住宅ローンは20年、30年は当たり前ですので、その間に発生する可能性はそれなりに高いのではないでしょうか。
下記にローン金利と残存期間別の毎月返済額と支払総額の早見表を作成しました。
金利上昇の影響を早見表で確認【金利・返済期間マトリックス】
金利が上昇した場合にローン返済額がどれくらい変化するか確認できます。
ローン残高1,000万円当たりの「毎月返済額」と「支払総額」です。
まず最初に「毎月返済額」です。
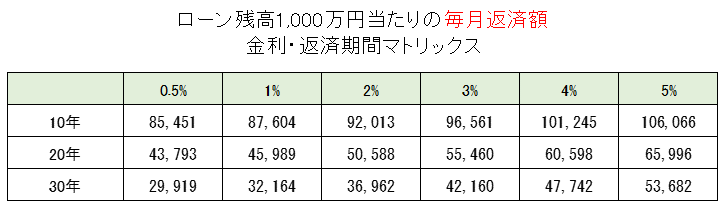
次に「支払総額」です。
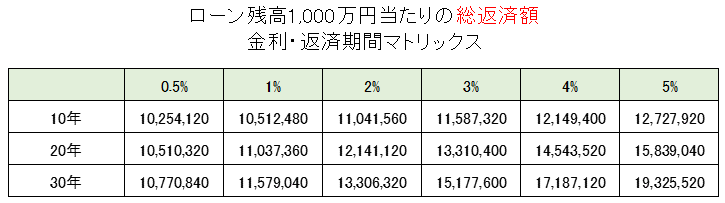
例えばローン残高が3,000万円の場合は3倍してください。
仮に悪いインフレで金利が上昇し、残存期間30年の時点で変動金利0.5%のローン金利が4%まで上昇したと仮定します。(ローン残高3,000万円)
- 0.5%の場合:29,919円×3=89,757円
- 4.0%の場合:47,742円×3=143,226円
金利が0.5%→4.0%に上昇すると毎月の返済金額は約1.6倍になります。
ローン残高が3,000万円の場合、毎月の返済額は約9万円から14万円以上まで上昇します。
このリスクは大きいです。
「こんなに金利が上がるわけない」と多くの人が考えるでしょうが、悪いインフレの場合はこれ以上の可能性もあります。
これをヘッジするには一部を固定ローンにして変動と固定のハイブリッドにするのが理想的です。(何事も分散が大切です)
よく、「金利が上がりはじめたら固定化する」という人もいますが、これは「株は下がりはじめたら売る」という人と同じでほとんどの場合、出来ませんので注意してください。
エクセルを使った「住宅ローン元利均等払い」のシミュレーション【PMT関数】
住宅ローンの返済シミュレーションをより具体的に計算したい方はEXCEL(エクセル)を使うと簡単に計算できます。
EXCELを使ったローン元利均等返済の金額を計算する方法を分かりやすく説明しますのでご覧ください。
エクセルの「PMT関数」を使います。
例)1000万円・30年(360ヶ月)・3%の元利均等払い
この条件で毎月の返済額を計算します。
エクセルを開きます。
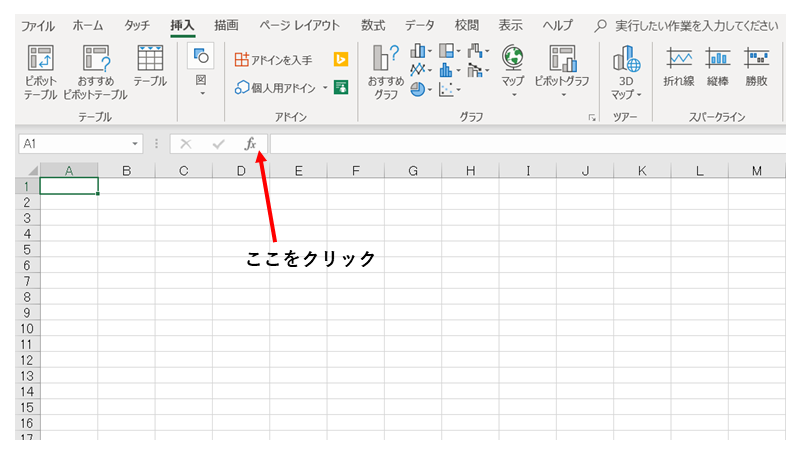
次にPMT関数を選択します。
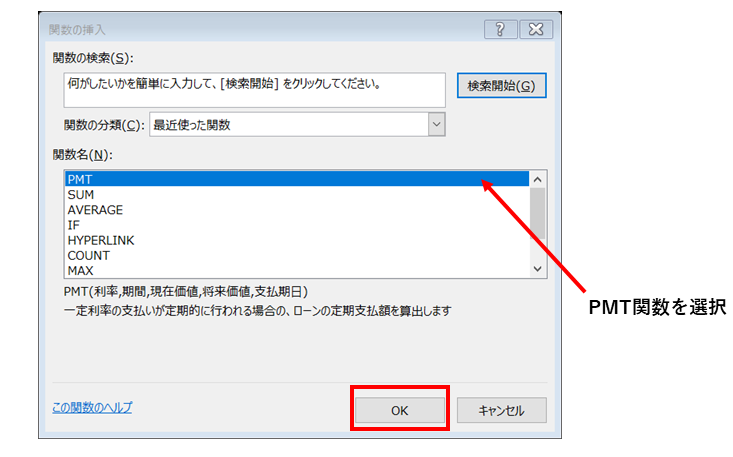
次に住宅ローンの条件を入力します。
PMT関数の入力項目は5つです。
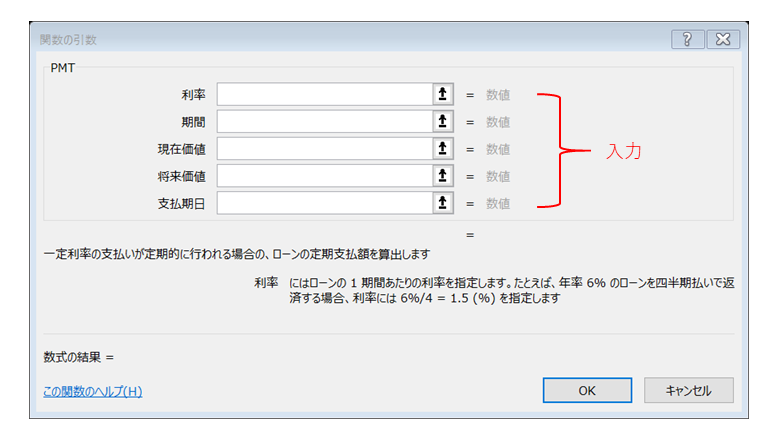
下記の通り入力します。
- 利率:3%/12(または0.0025)
- 期間:360
- 現在価値:10,000,000
- 将来価値:返済後の残金なので「0」を入力
- 支払期限:期首払いは「1」、期末払いは「0」または省力なので「0」を入力
上記を入力すると、エクセルのセル内の数式は下記のようになります。
=PMT(3%/12,360,10000000,0,0)
これで自動的に計算され、毎月の返済金額は「42,160円」と表示されます。
「42,160円」に「30年(360ヶ月)」をかけると返済総額の「15,177,600円」になります。
上記のマトリックスと一致します。
金利上昇リスクを考えながら、シミュレーションしてみてはいかがでしょうか。