こちらのページでは月次リターンのデータからEXCELを使って「年率リターン」「年率リスク(標準偏差・ボラティリティ)」「共分散」「相関係数」を簡単に計算する方法を紹介しています。
アセットクラスのリスク・リターン表を作成する場合などに役に立ちます。
月次リターンからEXCEL関数で「リターン」「リスク(標準偏差・ボラティリティ)」「共分散」「相関係数」を求める
先進国株式・先進国債券・新興国株式・新興国債券(現地通貨建て)の月次リターンをもとに「年率リターン」「年率リスク(標準偏差・ボラティリティ)」「共分散」「相関係数」を求めます。
まず各資産の月次騰落率の時系列データを準備します。
EXCELの関数を使うことで簡単に「年率リターン」「年率リスク(標準偏差・ボラティリティ)」「共分散」「相関係数」を求めることができます。
まずは「年率リターン」と「年率リスク(標準偏差・ボラティリティ)」です。
ちなみに運用の世界で「リスク」「標準偏差」「ボラティリティ」は同じもの指すと考えて差し支えありません。
- 「リスク」「標準偏差」「ボラティリティ」についてはこちらも参照:ボラティリティについての分かりやすくて詳しい説明
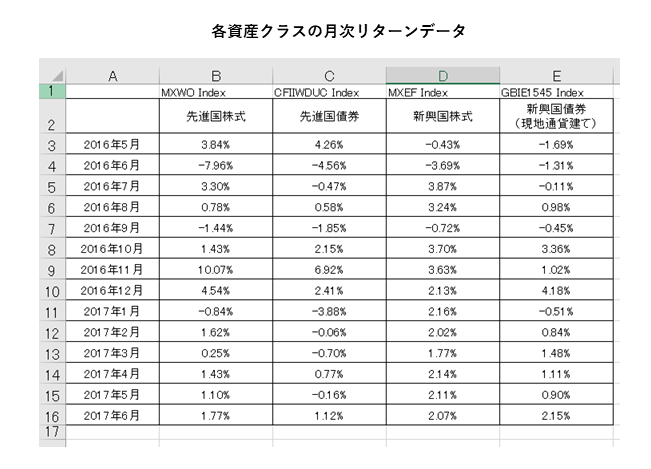
「年率リターン」の計算には「AVERAGE関数」、「リスク(標準偏差)」の計算には「STDEVP関数」を使います。
(ちなみにAVERAGE関数で計算する年率リターンはあくまで月次リターンの平均値を年率換算したものです。当該期間の年率パフォーマンスとは異なります。年率のパフォーマンスを計算したい場合はPOWER関数を使って計算することができます。)
セル内の数式は下記の通りです。「=(イコール)」の後に数式を入力します。
関数の後ろにSQRT(12)とありますが、これはルート12(√12)の意味で月次データを年率に変換するためにルート12を掛けます。
月次データを使って「年率リターン」や「年率リスク」を計算したい場合は忘れないようにしましょう。
上記のやり方で簡単にリスク・リターン表が作成できます。
次に「共分散」と「相関係数」です。
この2つは少しマニアックですが、念のために覚えておきましょう。
特に「相関係数」はポートフォリオの分散効果を考える場合に重要です。
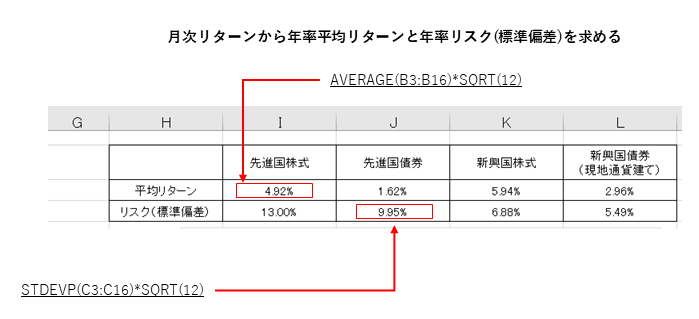
「共分散」は「COVARIANCE関数」、「相関係数」は「CORREL関数」を使います。
セル内の数式は下記の通りです。「=(イコール)」の後に数式を入力します。
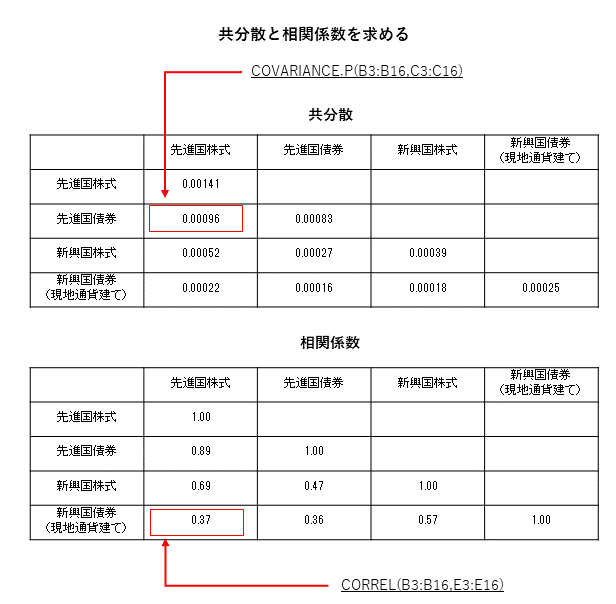
「共分散」や「相関係数」も上記のようにEXCELの関数を使えば容易に計算できますが、関係式を理解しておいた方が本当の意味が分かります。
「共分散」「標準偏差」「相関係数」の関係式です。
- AとBの共分散=「Aの標準偏差」×「Bの標準偏差」×「ABの相関係数」
ちなみに「相関係数」は2つの資産クラスの値動きの類似性を表す指標で-1~1の数値で表されます。
「相関係数」が1に近づくと2つの値動きが似ているということとなり、-1に近づくと真逆の値動きということになります。
ポートフォリオの分散効果を考える場合は、相関係数が「0」に近い方が値動きに関連性がないということになり、一般的に良いと考えられます。
「共分散」は上記式の通り、「相関係数」に2つの対象資産の「標準偏差」を掛けたものとなります。
言い換えると「共分散」は2つの対象資産の動きの類似性(相関係数)に変動率(ボラティリティ)を加味したものと言えます。
使用したインデックス
- 先進国株式:MSCIワールドインデックス(MXWO Index)
- 先進国債券:Citi World Government Bond Index (CFIIWDUC Index)
- 新興国株式:MSCIエマージング・マーケット・インデックス(MXEF Index)
- 新興国債券(現地通貨建て):JPモルガン・ガバメント・ボンド・インデックス・エマージング・マーケッツ(GBI-EM)グローバル・ディバーシファイド、キャップ15%フロア4.5% (GBIE1545 Index)
EXCELを使ったリスク・リターン表の作り方(散布図を活用)
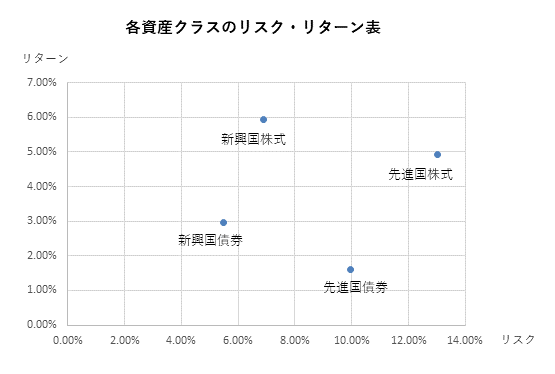
上記で計算した「年率リターン」「年率リスク(標準偏差・ボラティリティ)」のデータを使ってリスク・リターン表を作成します。
リスク・リターン表は各資産クラスの「年率リターン」と「年率リスク(標準偏差・ボラティリティ)」のデータからエクセルの図形作成で簡単にできます。
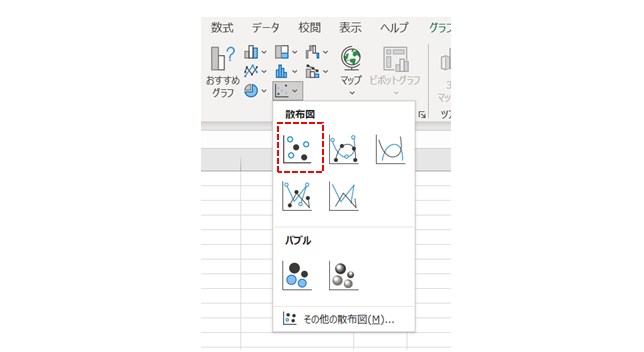
下記のリスク・リターン表を作成するにはEXCELの「挿入」→「グラフ」で「散布図」を使うと便利です。
ここからさらに進んで有効フロンティア曲線を作成することも可能ですが、少し難しいので今回は掲載しません。
散布図の作成が上手くいかない方は下記を参考にしてください。
リスク・リターン表の作成手順です。
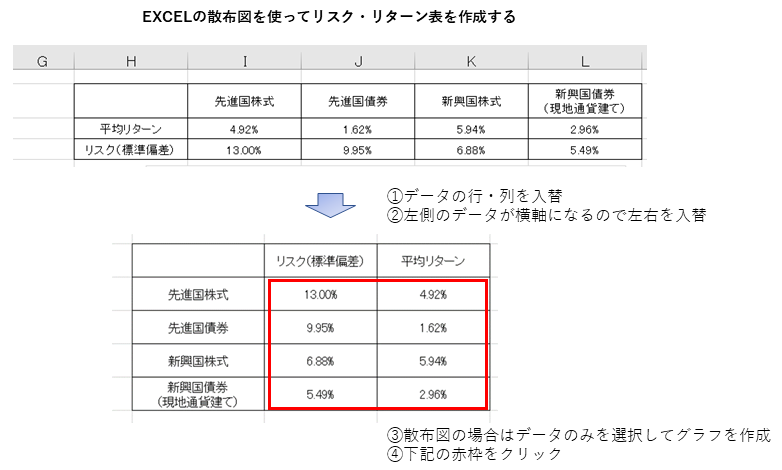
- データを並び替え(行と列、左と右)
- 範囲を指定(データ部分のみ)
- グラフウィザードの「散布図」で作成
散布図の作成は少しややこしいところがありますが、慣れれば問題ありません。
ちなみに過去のデータからリスク・リターンを計算する場合、リターンはどの期間のデータを使用するかで大きく変化しますが、リスク(標準偏差・ボラティリティ)は概ねどの期間を使っても資産クラスごとの特徴通りのデータとなります。
よって、機関投資家などで最適ポートフォリオを検討する際にはリスク(標準偏差・ボラティリティ)は過去のデータから計算したものを使い、リターンは過去データを使わずに予想される期待リターンや配当利回り・株式益利回りなどを使う場合も多くなっています。
また、リターンとリスクのデータから算出できる「シャープレシオ」というデータもよく利用されます。
「シャープレシオ」はリスク当たりのリターンを表す指標ですが、リターンは正確にはリスクフリーレートを控除したデータを使います。

仮に低金利の環境を想定し、リスクフリーレートをゼロとした場合、リターン/リスクとなり、各資産クラスのシャープレシオは上記のリスク・リターン表の傾きとなります。
上記のリスク・リターン表では新興国株式の傾きが最も急になることからシャープレシオが最も高いということになります。
新興国株式のリターン5.94%、リスク6.88%、仮にリスクフリーレート0%とするとシャープレシオは5.94/6.88=0.86となります。
ちなみによくリスクリターン表にヘッジファンドやPEファンドのデータを掲載してシャープレシオが高いと宣伝している資料を見かけますが、ヘッジファンド・PEファンドはリターンの分布が正規分布にならないため、本来、株式や債券などの伝統的アセットと一緒にリスクリターン表に掲載することはミスリードです。
リターン5%・リスク8%の意味を具体的に説明できますか?
リスク・リターン表で例えば「リターン5%・リスク8%」と言った場合、具体的に何を表しているか説明できる人は意外に少ないようです。
ここではリスク・リターン表の見方を解説します。
「リターン」はそのまま年率の収益率で問題ありません。
「リスク」は標準偏差のことです。
ちなみに標準偏差も良く使われるもので「1標準偏差」と「2標準偏差」があります。
少し難しくなるかもしれませんが、「1標準偏差」は正規分布において約68%の部分が収まる範囲で、「2標準偏差」は約95%の部分が収まる範囲です。
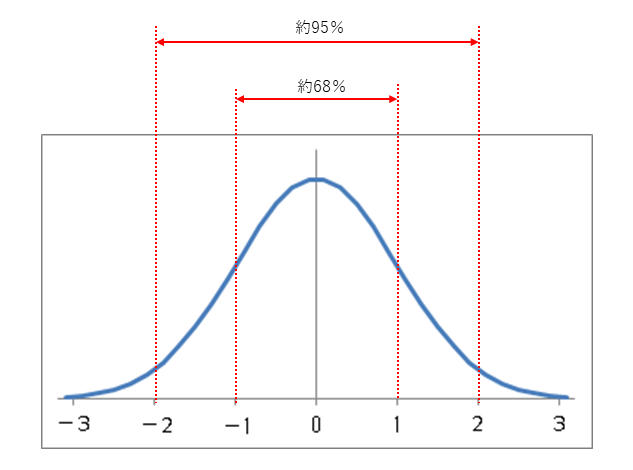
通常、投資の世界で「リスク」と言えば、特に指定がなければ「1標準偏差」のことを言います。
よって「リターン5%・リスク8%」は「5%±8% (つまり-3%~+13%)の範囲に約68%の確率で収まる」ことを表します。
これがリスク・リターンの本当の意味です。是非、覚えておいてください。
また、「標準偏差」は株式などのテクニカル分析で使われるボリンジャーバンドでも活用されます。
ボリンジャーバンドでは一般的には「2標準偏差」を使うことが多くなっています。
よって、2標準偏差のボリンジャーバンドは約95%の確率で収まる範囲ということになります。
「1標準偏差」「2標準偏差」のことを「1σ(シグマ)」「2σ(シグマ)」と呼ぶこともあります。
機関投資家向け営業の世界では当たり前の話かもしれませんが、リテール向け営業ではこのリスクリターンの意味を理解している方が少ないと感じた為、掲載しました。