こちらのページでは債券投資で重要な「デュレーション」について事例を挙げながら分かりやすく解説しています。
デュレーションには「マコーレーデュレーション=平均回収期間」と「修正デュレーション=金利感応度」の2種類があります。
いずれも単にデュレーションと呼ばれることも多いため、違いをよく理解していない方も多いようです。
一般投資家にとってより重要なのは金利感応度(金利が1%変動した場合に債券価格が何%変動するか)ですので「修正デュレーション」はよく理解しておくべきです。
詳細は下記をご覧ください。
2つのデュレーション
デュレーションには2種類あります。
- マコーレーデュレーション【平均回収期間】
- 修正デュレーション【金利感応度】
正式な名称は上記の通りですが、ややこしいのが、両方とも単に「デュレーション」と呼ばれることも多くあります。
マコーレーデュレーション=平均回収期間
マコーレーデュレーションは債券に投資した資金の「平均回収期間」を表します。
(※正確には将来キャッシュフローの現在価値が投資元本になるまでの期間です)
一般的な債券(利付債)の「平均回収期間」は残存期間より少し短い期間となります。
残存期間・最終利回りが同じでもクーポンが高いと回収期間が短くなるので、マコーレー・デュレーションは短くなります。
ゼロクーポン債の場合は「残存期間=マコーレーデュレーション」となります。
修正デュレーション=金利感応度
修正デュレーションの計算式はこのようになります。
- 修正デュレーション=マコーレーデュレーション /(1+最終利回り)
ここで言う金利感応度とは具体的には「市場金利が瞬間的に1%上昇した場合の債券価格の変化率」であり、修正デュレーションが長いと債券価格の変化率は高まります。
つまり、修正デュレーションが長いと金利が上昇した場合の債券の下落率が大きくなります。(もちろん金利が低下した場合は債券価格の上昇率が大きくなります)
仮に修正デュレーション5年の債券があった場合、瞬間的にマーケット金利が1%上昇したとき、この債券の価格は5%下落することになります。
また、クーポンの水準にもよりますが、一般的に修正デュレーションは債券の残存期間よりやや小さい数字となります。
こちらはデュレーションと債券価格のイメージ図です。
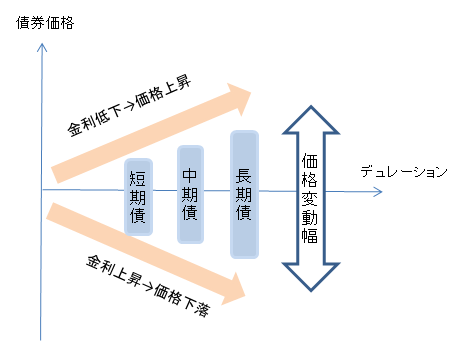
債券の残存期間が長くなると修正デュレーションが長くなり、金利感応度が大きくなることで、金利変動による債券価格の変動が大きくなります。
投信の月次レポート等、債券の金利感応度を表現する際は単にデュレーションと書かれていても、修正デュレーションを表しているはずです。
デュレーションの事例(10年米国ストリップス債)
一般投資家がデュレーションを気にするのは金利感応度(金利の変化に対する債券価格の変化)を考える場合だと思います。
ここでは10年米国ストリップス債を例に解説します。
米国ストリップス債とはゼロクーポンの米国債です。
ここでは10年米国債の利回りが4%と仮定します。
まず、ゼロクーポン債ですので「マコーレーデュレーション」は「残存期間」と同じになります。
- マコーレーデュレーション=10年
そして金利感応度を表す「修正デュレーション」は『修正デュレーション = マコーレーデュレーション /(1+最終利回り)』ですので下記の計算となります。
- 修正デュレーション=10年/1.04=9.62年
- 米ドル金利が1%低下した場合、債券価格は9.62%上昇
- 米ドル金利が1%上昇した場合、債券価格は9.62%下落
このように金利感応度(金利の変化に対する債券価格の変化)を分析したい場合は「修正デュレーション」を確認しましょう。
関連ページ
その他の債券の知識についてはこちら!
債券市場の全体像はこちらを参照!